Whitepaper: Optical Physics

Digital Sensor Characterization

A rigorous look at quantum efficiency, photon transfer curves, and characterizing sensor performance in a home laboratory setting.

1. The Architecture of Modern Capture

+-------------------------------------------------------------------+
|               BACK-ILLUMINATED (BSI) PIXEL ARRAY                 |
|               - Micro-lenses & Color Filter Array (Bayer)         |
|               - 100% Fill-Factor Silicon Photodiode Layer         |
+-------------------------------------------------------------------+
                                  ||  (Cu-Cu Direct Bond Interconnects)
+-------------------------------------------------------------------+
|               HIGH-SPEED DIGITAL LOGIC & ADC LAYER                |
|               - Parallel Column-Parallel ADC Units                |
|               - High-Speed MIPI CSI-2 Serialization Logic          |
+-------------------------------------------------------------------+
Fig 1.1: Schematic cross-section of a 3-layer Stacked CMOS sensor with Cu-Cu interconnects.

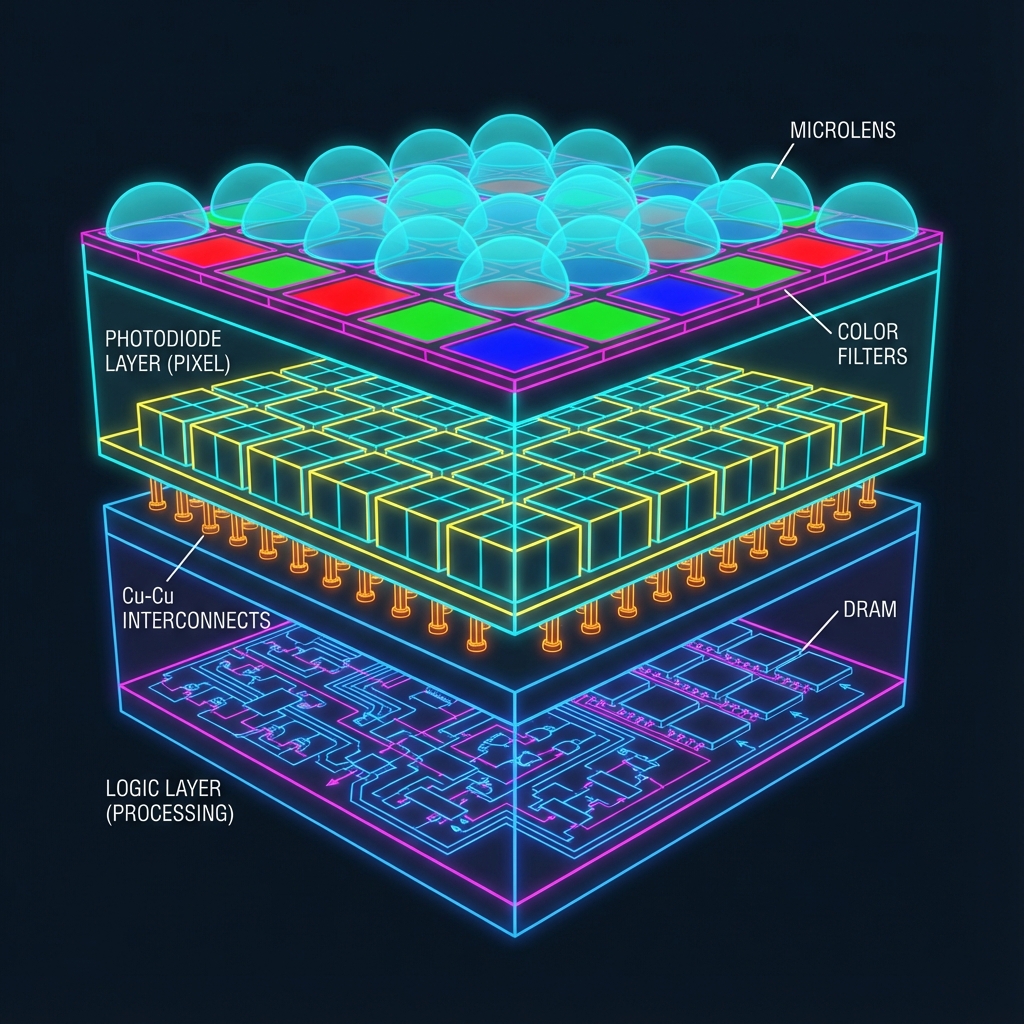
Over the past 20 years, the industry has engineered sensors for the world's most demanding optical systems—from Leica's rangefinders to Hasselblad's medium format backs. The shift from CCD to CMOS was pivotal, but the true revolution lies in the Stacked Back-Illuminated (BSI) architecture shown above.

In modern Sony sensors, we separate the photodiode layer from the logic/processing layer. This allows us to maximize the fill factor of the pixels (capturing more photons) while simultaneously using a high-speed logic process node for the readout circuitry beneath. The Cu-Cu (Copper-to-Copper) interconnects provide the high-density vertical electrical pathways needed to parallelize readout, essentially eliminating the "rolling shutter" effect in our latest designs.

2. The Photon Transfer Curve (PTC)

Decoding the Signal

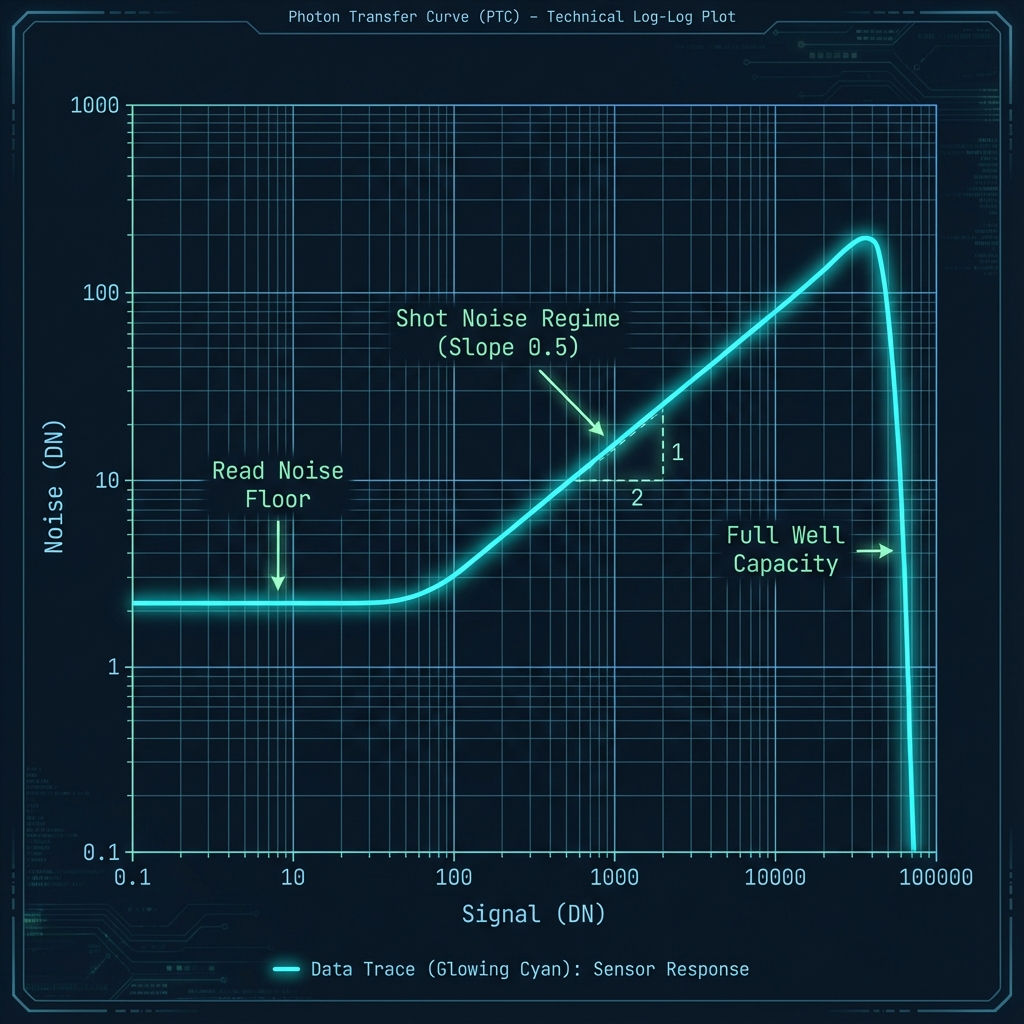
The Photon Transfer Curve (PTC) is the "heartbeat" of any image sensor. It plots the noise (standard deviation) against the signal (mean) on a log-log scale. This single plot reveals the three fundamental operating regimes of the device:

  • Read Noise Regime: The flat floor on the left. This is the electronic noise inherent to the readout chain, independent of light.
  • Shot Noise Regime: The slope of 0.5 (or 1/2). Here, photon statistics dominate. Noise scales with the square root of the signal ($\sigma = \sqrt{S}$).
  • Full Well Saturation: The sharp drop-off on the right. The pixel is full, variance collapses because every pixel reads the maximum value. 
Noise (Log σ)
  ^
  |        Shot Noise (Slope 1/2)
  |              /--------\  Full Well
  |             /          \ Saturation
  |  ----------/
  |  Read Noise Floor
  +---------------------------------->
  0                                Signal (Log S)
Fig 2.1: Idealized Photon Transfer Curve (PTC) log-log regimes.

3. Experiment: Generating Your Own PTC

You do not need a million-dollar lab to characterize your camera. You can generate a PTC using a standard digital camera capable of shooting RAW.

Equipment Required

Procedure

STEP 1: Set camera to base ISO. Turn off all noise reduction and lens corrections.

STEP 2: Defocus the lens completely on the flat light source. We want a uniform field, not an image of the pixels.

STEP 3: Shoot a series of pairs.
- Pair 1: 1/8000s (Black frame/Read noise)
- Pair 2: 1/4000s
- ...
- Pair N: 1s (Saturation)

STEP 4: Analyze.
For each pair, calculate the mean signal ($S$) and the variance ($\sigma^2$). Plot $\log(\sigma)$ vs $\log(S)$.

Python Analysis Snippet

Use the following snippet to process a pair of RAW files:

import rawpy import numpy as np import matplotlib.pyplot as plt def analyze_pair(file1, file2): raw1 = rawpy.imread(file1).raw_image_visible.astype(float) raw2 = rawpy.imread(file2).raw_image_visible.astype(float) # Difference image removes Fixed Pattern Noise diff = raw1 - raw2 # Calculate noise (std dev of difference / sqrt(2)) noise = np.std(diff) / 1.414 signal = np.mean(raw1) return signal, noise

4. Interactive Simulations

Sensor architecture is best understood through experimentation. Use these interactive modules to simulate fundamental physical properties of image capture.

Sim 1: The Photon Rain (Shot Noise)

Photon arrival is a Poisson process. As light levels drop, the "rain" of photons becomes sparse, creating visible noise.

Target Signal (Photons/Pixel): 1000
Calculated SNR (dB): 30.0
Visual simulation of Poisson noise. Notice how noise dominates at lower signal levels.

Sim 2: Dynamic Range Architect

Design your own sensor pixel. Adjust the Full Well Capacity (FWC) and Read Noise to see the theoretical Dynamic Range.

30000 e-
2.5 e- RMS
RESULTING DYNAMIC RANGE
81.6
dB
Formula: 20 * log10(FWC / ReadNoise)